Vedic Mathematics
at the 16th World Sanskrit Conference, Bangkok
29th June to 30th June 2015

Vedic Mathematics Panel – World Sanskrit Conference

Abstracts

1. Challenges to assimilating Vedic Math in the math classroom
Swati Dave
As proponents of Vedic Math our ultimate goal and dharma is to reveal the beauty of this ancient mathematical system to the world. Every child should have the opportunity to study this simple, fast, and easy form of math.
The only way to achieve this is to integrate Vedic Math into the K-12 math curriculum. Some of the Vedic Math advocates are working hard with curriculum planners, teachers, parents and educational authorities, to make this happen. A few have succeeded, but most have not.
I intend to share the stories of people who have succeeded, and also find the reasons why most are still struggling.
In this paper, I aim to find the percentage of impact of the many overt challenges to integrating Vedic Math, such as the common misconception that Vedic Math is just a set of tricks, the dearth of good resource materials, the lack of formal training for teachers of Vedic Math, the hesitancy of the decision makers to try a novel, unconventional way of teaching, and the paucity of research statistics proving the benefits of Vedic Math. I also intend to go beyond the obvious and attempt to determine if there are indeed any limitations to Vedic Math that are preventing it from reaching its rightful place in the math world.
I wish to understand the challenges and learn from the successes in order to create a plan that offers a practical solution for the global assimilation of Vedic Math in to the math classroom.

2. Vedic Maths as a Pedagogic Tool
James Glover & Kenneth Williams
The characteristics of Vedic mathematics lead to a teaching and learning approach that has many advantages over conventional pedagogies. These include speed, creativity, flexibility and the development of strategy skills in problem solving. Due to exam syllabus requirements students often merely follow rules for solving problems at the expense of understanding. However, the Vedic approach enables students, not only to excel in their learning and exam performance, but also to enjoy the subject and to explore and apply their own creativity. The sutra-based system contains simple yet subtle principles each with multifarious applications. This enables pattern-recognition to develop across different topics.
One of the most sort after uses of mathematics education is the training it can provide in managing problems using alternative strategies. This is one of the hallmarks of Vedic mathematics, for not only does it have over-arching methods, but also special case methods which are brought to bear when dealing with particular problems.
This paper provides examples showing the properties and qualities of Vedic Maths and discusses why it is a valuable pedagogic tool.

3. Adapting Vedic Mathematics in modern technology and learning analytics: enhancing creativity and efficiency in math
Lokesh Tayal
In the last few decades, we have seen tremendous and progressive growth in the field of mathematics. Most of this development has occurred in the domain for higher mathematics; this can be observed through several mathematic symbols being constantly created and used by researchers. However, there is limited research and growth in the field of elementary mathematics. Children learn elementary math through a rigid structure whereby they ultimately lose interest in math. This is where Vedic Mathematics is of considerable benefit, as it provides an avenue that inculcates interest and creativity in math for children.
We have developed a state of the art software application that generates Vedic math worksheets. Children attempt these worksheets and all their learning parameters are captured in real time in our user-friendly software. This software also triggers collaboration between students, parents and teachers. All the learning data is analyzed in detail to allow for quick and easy assessment and advancement. We have also obtained feedback and conducted scientific studies to demonstrate that children who learn Vedic Mathematics are highly efficient, highly creative and achieve a better understanding of numbers and patterns.
This paper aims at demonstrating the value of Vedic Mathematics through the system of learning data that is captured. It also aims to determine that Vedic Math will enhance the creativity and efficiency in math for our future generations to come.

4. The Magic of the last digit
Robert McNeil
In Chapter 35 of Vedic Mathematics, Tirthaji lays out a delightful method for extracting the cube root of exact cubes by using the sutra Vilokanam (observation) and by argumentation (Vitarka).
The method highlights the significance of the last digit which uniquely indicates the final digit of the cube root for odd numbers and is easily adapted for even numbers. The link between the final digit of cube root and the final digit of the exact cube is revealing in its simplicity. Even more dramatic however is the revelation that for certain higher powers, the last digit of the power is identical with the last digit of the root. For example the 5th root of 14348907 ends in 7. This in turn enables 5th roots of exact 5th powers to be extracted “by mere observation” using Vilokanam.
This paper will expand Tirthaji’s simple method for finding cube roots to other higher powers and illuminate the order of the final digit in all powers.

5. Contribution of Indian Mathematics to the world
Daya Tiwari
The wealth of ancient Indian Mathematical Science has contributed a lot to the world civilization . Ironically, modern India seems to have forgotten its rich ancient heritage treasure preserved in the vast Sanskrit literature. The Science of Mathematics, with all its branches such as Arithmetic , Algebra , Geometry and Trigonometry, etc., was so well developed in ancient India that many modern scholars find to their dismay that some of the European discoveries has already been discovered long ago . It is the need of hour to integrate this valuable treasure of Indian scientific knowledge with that of modern science. India has the unique distinction of combining the three concepts - 1. decimal system 2. place value and 3. a computational zero (shunya) . The origin of Geometry is from Shulvashutra .

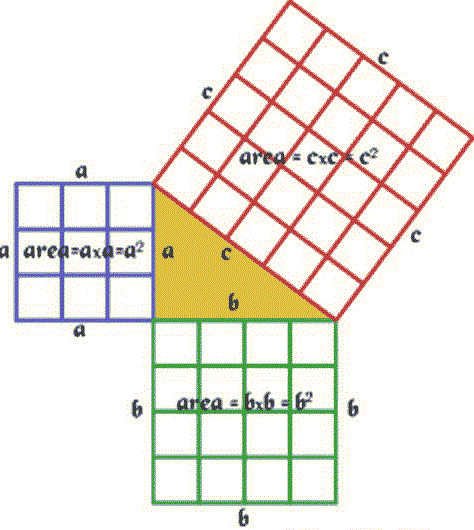
The equation c2=a2+b2, which is known as Pythagoras’ theorem, was first given by Baudhayana (800 BC) before Pythagoras (580-500 BC) . This is basically shulva theorem (Baudhayana Shulvashutra , 1-48) .There is clear reference of numbers in the Vedas . In the Rigveda, we find one and twenty numbers (Rigveda; 7.18.11) Ten and hundred numbers (Rigveda; 6.47,22-24) In the Yajurveda , the powers of 10 from 10 to the power 10 and 10 to the power 12 is listed . (Yajurveda 17.2 ). Arithmetic progression (AP) i.e. series of multiples of 4 is mentioned in the Yajurveda (18.25) . Numbers with the description of Ayut (10,000) and Nyarbud (ten crorers) are in the Atharvaveda (8.8.7) . Valmiki Ramayana (kanda 6th sarga 28 , shloka 33-43) mentions not only the strength of Rama but also establishes a relation between the numbers .
In Aryabhatiyam (Ganitpada , 10) , Aryabhatta 1st (476 AD) has given the value of p as 3.1416 , which is correct to four decimal places and it has been universally accepted .
This research paper is aimed at determining the mathematical facts with examples and proofs from various ancient Sanskrit texts . There shall also be a special focus on the blend of ancient Indian mathematics and universal modern mathematics.

6. Geometry in Ma??alas and Yantras
Vanishri Bhat
Geometry in ancient India dates back prior to 800th BCE, where altars of different shapes and sizes were needed to be constructed in order to perform yagas and yajnas. Basic geometrical figures such as triangles, squares, circles, hexagons etc., were very common structures in building altars. As a part of performing Vedic rituals, in almost all sacrifices, the tradition of drawing Ma??alas or Yantras are seen. These Ma??alas, being an essential part of the rituals, also consist of few basic geometrical shapes along with a few natural colours filled within.
In our paper we will discuss different geometrical patterns that appear in Ma??als, their significance and their relevance in srauta karmas. Sometimes we see very simple sketches, for example underlying grids are drawn or sometimes more complicated structures such as Sudrashana ma??als. The srauta sutras prescribe the construction of these prior to performing rituals. We will try to investigate whether Ma??als and Yantras, which are drawn during rituals, are related geometrically to altars.

7. An Investigation into the Working of the Ekadhikena Purvena Sutra, and how it can be used to identify Prime Numbers
Marianne Fletcher
The identification of very large prime numbers is of considerable importance in fields such as cryptology and coding in security systems. Two of the Vedic mathematics sutras expounded by Sri Bharati Krishna Tirtha can be employed in the search for such large primes.
The Ekhadikena Purvena sutra, By one more than the previous one, can be used to calculate all the digits in the recurring decimal string of any non-terminating rational number. The arithmetic operation is based on the fact that the digits in any such decimal string are, in fact, consecutive terms of a geometric sequence: so, if the common ratio (the “ekhadika”) can be found, so can the decimal string. The computation is further simplified by application of the Nikhilam Navatascaramam Dasatah sutra, which easily generates the second half of the decimal string once the first half has been found.
Investigations into the patterns and cyclical lengths of decimal strings thus generated point to a useful application with regards to identifying whether the denominator N (of rational number 1/N) is prime or not. If x is the number of digits before recurrence, and if (N-1) is not divisible by x, then N is not a prime number. However if (N-1)/x yields a whole number, N is almost always prime. An additional simple test can then be employed to verify the prime status, or not, of N.
The prime number test is based on determining the number (x) of digits in the decimal string of 1/N using the two sutras mentioned above.
It is suggested that further investigations be done, perhaps by other applications of these sutras, to find a quicker was of determining x without necessarily having to determine all the digits in a string.

8. Multiplication techniques: Ancient Indian methods vis-à-vis Vedic Maths methods of Tirthaji
Arvind Prasad
India holds a rich tradition in mathematics dating back for 2000 years and more. Arithmetic operations of addition, subtraction, multiplication, division etc., form part of Indian mathematics called Paati-ganita. The Bakhshaali manuscripts (200 A.D.) and Trishatikaa (750 A.D.), etc., deal exclusively with the paati-ganita techniques. Moreover, sections on mathematics are contained in many ancient texts on astronomy, such as the Shulba sutras (~500 B.C.), as well as in individually authored texts such as the Aryabhatiya (by Aryabhata I – 499 A.D.).

Recently, Bharathi Krishna Tirthaji (BKT) wrote about 16 sutras and 13 upasutras in his seminal work, Vedic Mathematics, first published in 1965. It is claimed that these sutras describe the natural way the mind works when dealing with numbers and thus cover all of mathematics. Thus, the applications of the sutras range from simple arithmetic operations of addition and subtraction to the more advanced subjects of coordinate geometry and calculus.
It is of great interest to test if the recently proposed sutras of Vedic Maths from the last century can be extended to the mathematics of the ancient times. In this paper the seven ancient methods of paati-ganita multiplication are compared with BKT’s Urdhva Tiryagbhyamam sutra (translated as Vertically and Crosswise), which forms the general method of multiplication in the Vedic Maths system. The comparison reveals that one of the ancient methods, Cross-Multiplication, indeed shows a one-to-one match with the Vertically and Crosswise method of BKT. Furthermore, the application of some of the other sutras and upasutras of Vedic Maths such as Purnapurnabhyam, Yavadunam and Anurupyena can be extended to other ancient Indian multiplication techniques.

9. Vyashti Samashti – A sutra from Sankaracarya Bharati Krishna Tirtha
James Glover
This mathematical sutra from the Vedic Mathematics of Sankaracarya Sri Bharati Krishna Tirtha has manifold applications in algebra, induction, statistics, dynamical geometry and chaos theory. It describes how the form of the whole is reflected in the specific or individual. It also has much wider significance as it reflects a common philosophical principal in many ancient and modern traditions. This principle is found in teachings from Vedanta, ancient Egypt, Christianity, Hermeticism, Judaism, Platonism and several others. One of the important characteristics of Vedantic philosophy is that the practical and spiritual are not separate but are interrelated and holistic. This sutra provides a prime example of how practical knowledge is related to a spiritual principle.
This paper explores some of the mathematical applications of the sutra and aspects of the philosophical meaning in terms of how the Samashti, or Universal, is reflected within the Vyashti, Individual.

10. Vedic Mathematics (of Swami Shree Bharatikrishnatirthaji Maharaj, Jagad Guruji)
Sujauddin Shaikh
People find difficulty in addition & subtraction, multiplication – vilokanan, Urdhva Tiryagbhyam, Ekadhikena and Eka Nyunena Purvena. Use of Nikhil, Paravartya, Flag No. for division.
Square:- of Nikhilam., by Anurupuyena, Duplex Cube by ratio method and Yavadunam, Square root and Cube root by operation general method. General roots of Divisibility. People need to utilize more time these process which are know us “ PARI KRAMASHTAKAM” in Sanskrit. Holy Saint Swami Shri Bharati Krishna Tirthji Maharaj, Shankrachariya of Jagannathpuri thought deeply and tried to utilize Algebra for simplifying this process and constructed 16 sutras (Formula) and 13 up sutras (Sub-Formula) and wrote a book on “Vedic Mathematics”. Its Magic Effect of speedy calculation are very much pleasing. People ask for the proof where these methods are in holy “Atharva Veda” or any other Veda. In fact swamiji studying Sulabh Sutras in Atharva Veda. Which are in Sanskrit. He use Sanskrit Sloka Method and he named it Vedic Mathematics. In European Countries it is propagated. In fact Vedic Mathematics possesses some technique based on mathematical facts which help to make the calculations simple and easy to save the time. Jagad Guruji Swami Krishna Tirathji Maharaj named us Venkat Raman was extra ordinary proficient in Sanskrit and oratory and on account this he was awarded the title of “SARASWATI” by the madras Sanskrit Association in July 1899, when he was still in his 16th year. He started his pubic life under the guidance of late Hon’ble Shri Gopalkrishna Gokhle, C.I.E. in 1905 in connection with the National Education Movement and the south African Indian issue He. Also spent in the profoundest study of the most advance Vedanta Philosophy and practice of the Brahma-sadhna.